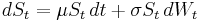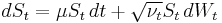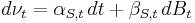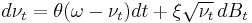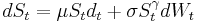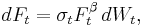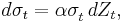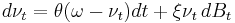Stochastic volatility

See also Volatility (finance).

Stochastic volatility models are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the underlying security, the tendency of volatility to revert to some long-run mean value, and the variance of the volatility process itself, among others.

Stochastic volatility models are one approach to resolve a shortcoming of the Black–Scholes model. In particular, these models assume that the underlying volatility is constant over the life of the derivative, and unaffected by the changes in the price level of the underlying security. However, these models cannot explain long-observed features of the implied volatility surface such as volatility smile and skew, which indicate that implied volatility does tend to vary with respect to strike price and expiry. By assuming that the volatility of the underlying price is a stochastic process rather than a constant, it becomes possible to model derivatives more accurately.

Contents

Basic model

Starting from a constant volatility approach, assume that the derivative's underlying price follows a standard model for geometric brownian motion:

dS_t = \mu S_t\,dt %2B \sigma S_t\,dW_t \,

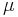where \mu \, is the constant drift (i.e. expected return) of the security price 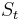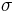S_t \,, \sigma \, is the constant volatility, and 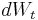dW_t \, is a standard Wiener process with zero mean and unit rate of variance. The explicit solution of this stochastic differential equation is

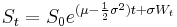S_t= S_0 e^{(\mu- \frac{1}{2} \sigma^2) t%2B \sigma W_t}.

The Maximum likelihood estimator to estimate the constant volatility \sigma \, for given stock prices S_t \, at different times t_i \, is

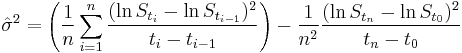\hat{\sigma}^2= \left(\frac{1}{n} \sum_{i=1}^n \frac{(\ln S_{t_i}- \ln S_{t_{i-1}})^2}{t_i-t_{i-1}} \right) - \frac{1}{n^2} \frac{(\ln S_{t_n}- \ln S_{t_0})^2}{t_n-t_0} ;

its expectation value is E \left[ \hat{\sigma}^2\right]= \frac{n-1}{n} \sigma^2.

This basic model with constant volatility 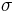\sigma \, is the starting point for non-stochastic volatility models such as Black–Scholes and Cox–Ross–Rubinstein.

For a stochastic volatility model, replace the constant volatility 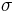\sigma \, with a function 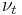\nu_t \,, that models the variance of 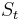S_t \,. This variance function is also modeled as brownian motion, and the form of 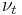\nu_t \, depends on the particular SV model under study.

dS_t = \mu S_t\,dt %2B \sqrt{\nu_t} S_t\,dW_t \,
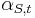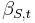d\nu_t = \alpha_{S,t}\,dt %2B \beta_{S,t}\,dB_t \,

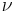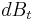where \alpha_{S,t} \, and \beta_{S,t} \, are some functions of \nu \, and dB_t \, is another standard gaussian that is correlated with 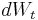dW_t \, with constant correlation factor \rho \,.

Heston model

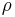Main article: Heston model

The popular Heston model is a commonly used SV model, in which the randomness of the variance process varies as the square root of variance. In this case, the differential equation for variance takes the form:

d\nu_t = \theta(\omega - \nu_t)dt %2B \xi \sqrt{\nu_t}\,dB_t \,

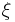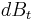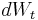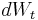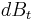where \omega is the mean long-term volatility, \theta is the rate at which the volatility reverts toward its long-term mean, \xi is the volatility of the volatility process, and dB_t is, like dW_t, a gaussian with zero mean and unit standard deviation. However, dW_t and dB_t are correlated with the constant correlation value \rho.

In other words, the Heston SV model assumes that the variance is a random process that

  1. exhibits a tendency to revert towards a long-term mean \omega at a rate \theta,
  2. exhibits a volatility proportional to the square root of its level
  3. and whose source of randomness is correlated (with correlation \rho) with the randomness of the underlying's price processes.

CEV Model

Main article: Constant Elasticity of Variance Model

The CEV model describes the relationship between volatility and price, introducing stochastic volatility:

dS_t=\mu S_t d_t %2B \sigma S_t ^ \gamma dW_t

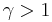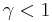Conceptually, in some markets volatility rises when prices rise (e.g. commodities), so \gamma > 1. In other markets, volatility tends to rise as prices fall, modelled with \gamma < 1.

SABR volatility model

Main article: SABR Volatility Model

The SABR model (Stochastic Alpha, Beta, Rho) describes a single forward F (related to any asset e.g. an index, interest rate, bond, currency or equity) under stochastic volatility \sigma:

dF_t=\sigma_t F^\beta_t\, dW_t,
d\sigma_t=\alpha\sigma^{}_t\, dZ_t,

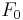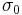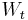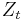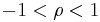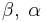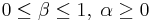The initial values F_0 and \sigma_0 are the current forward price and volatility, whereas W_t and Z_t are two correlated Wiener processes (i.e. Brownian motions) with correlation coefficient -1<\rho<1. The constant parameters \beta,\;\alpha are such that 0\leq\beta\leq 1,\;\alpha\geq 0.

The main feature of the SABR model is to be able to reproduce the smile effect of the volatility smile.

GARCH model

The Generalized Autoregressive Conditional Heteroskedasticity (GARCH) model is another popular model for estimating stochastic volatility. It assumes that the randomness of the variance process varies with the variance, as opposed to the square root of the variance as in the Heston model. The standard GARCH(1,1) model has the following form for the variance differential:

d\nu_t = \theta(\omega - \nu_t)dt %2B \xi \nu_t\,dB_t \,

The GARCH model has been extended via numerous variants, including the NGARCH, TGARCH, IGARCH, LGARCH, EGARCH, GJR-GARCH, etc.

3/2 model

The 3/2 model is similar to the Heston model, but assumes that the randomness of the variance process varies with 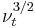\nu_t^{3/2}. The form of the variance differential is:

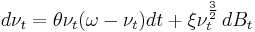d\nu_t = \theta\nu_t(\omega - \nu_t)dt %2B \xi \nu_t^\frac{3}{2}\,dB_t \,.

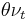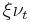However the meaning of the parameters is different from Heston model. In this model both, mean reverting and volatility of variance parameters, are stochastic quantities given by \theta\nu_t and \xi\nu_t respectively.

Chen model

In interest rate modelings, Lin Chen in 1994 developed the first stochastic mean and stochastic volatility model, Chen model. Specifically, the dynamics of the instantaneous interest rate are given by following the stochastic differential equations:

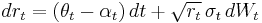dr_t = (\theta_t-\alpha_t)\,dt %2B \sqrt{r_t}\,\sigma_t\, dW_t,
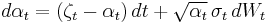d \alpha_t = (\zeta_t-\alpha_t)\,dt %2B \sqrt{\alpha_t}\,\sigma_t\, dW_t,
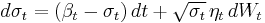d \sigma_t = (\beta_t-\sigma_t)\,dt %2B \sqrt{\sigma_t}\,\eta_t\, dW_t.

Calibration

Once a particular SV model is chosen, it must be calibrated against existing market data. Calibration is the process of identifying the set of model parameters that are most likely given the observed data. This process is called Maximum Likelihood Estimation (MLE). For instance, in the Heston model, the set of model parameters 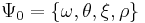\Psi_0 = \{\omega, \theta, \xi, \rho\} \, can be estimated applying an MLE algorithm such as the Powell Directed Set method [1] to observations of historic underlying security prices.

In this case, you start with an estimate for 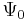\Psi_0 \,, compute the residual errors when applying the historic price data to the resulting model, and then adjust 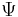\Psi \, to try to minimize these errors. Once the calibration has been performed, it is standard practice to re-calibrate the model over time.

See also

References

Options
Terms
Swaps
Forwards and Futures
Other derivatives
Market issues
Modelling volatility
Trading volatility